We talk about a current (best-paper award) publication at ACM-SIAM Symposium on Discrete Algorithms (SODA24) which provides a near-linear operating time deterministic algorithm for the elemental optimization drawback of discovering a minimal reduce in weighted graphs.
A graph is a ubiquitous knowledge construction utilized in laptop science that consists of nodes (or vertices) and edges between pairs of nodes to seize objects and their relations. The minimal reduce drawback (also known as “min-cut”) is a primary structural query in regards to the connectivity of a graph that asks: what’s the least costly option to disconnect a community? Extra formally, given an enter graph the place edges have no orientation (i.e., the graph is undirected) and are related to optimistic weights quantifying the significance of the perimeters (e.g., capability of a highway, or energy of a relationship, stage of similarity between the endpoints, and so forth.), a reduce is a partition of the nodes into two sides. The scale of a reduce is the overall weight of edges connecting nodes on completely different sides of the reduce, and the min-cut drawback is to discover a reduce of the minimal measurement.
Fixing it effectively has been some of the basic issues in algorithmic graph idea. Furthermore, min-cut has numerous functions in apply equivalent to picture restoration, stereo and segmentation in laptop imaginative and prescient, and community resilience evaluation (equivalent to for roads or energy grids). It is usually typically very helpful when the underlying graph knowledge is simply too giant and must be partitioned into smaller elements to be processed in a divide-and-conquer method.
Within the idea of algorithm design, the asymptotic complexity for any drawback that requires studying the whole enter (which is the case for min-cut) is at the very least linear within the measurement of the enter (since that’s the time wanted to learn the enter). A nearly-linear time algorithm primarily achieves this lower-bound, and thus is canonically seen because the optimum consequence one can obtain. For the min-cut drawback, current nearly-linear time algorithms are both randomized (which can output an incorrect reply with some chance) or solely work for the particular case when the graph is easy (which can not mannequin many real-world functions), so its optimum complexity stays an open drawback.
In “Deterministic Close to-Linear Time Minimal Reduce in Weighted Graphs”, which co-won one of the best paper award on the ACM-SIAM Symposium on Discrete Algorithms (SODA2024), we design the primary nearly-linear algorithm for the min-cut drawback that’s deterministic (i.e., all the time finds the proper reply) and that additionally works for common graphs, thus settling the optimum complexity for the min-cut drawback.
Technical insights
Our result’s the fruits of a protracted line of analysis, and algorithmic advances on this drawback (together with ours) are normally motivated by structural discoveries of graph connectivity. Specifically, a seminal consequence by Karger in 1996 gave a nearly-linear time randomized algorithm that finds a min-cut with excessive chance, and a important perception from that work was the existence of a a lot smaller graph that largely preserves all cuts’ measurement. That is helpful since one can afford to run a slower algorithm with the smaller graph as enter, and the slower operating time (by way of the scale of the smaller graph) can nonetheless be nearly-linear within the measurement of the unique (bigger) graph. Certainly, most of the structural discoveries on the min-cut drawback are alongside this path, and the high-level concept of lowering drawback measurement whereas preserving constructions of curiosity has been broadly impactful in algorithm design.
Reduce-preserving graph sparsification
We begin by discussing the structural perception utilized by Karger in additional element. Beginning with a graph G with n nodes, the cut-preserving sparsification by Benczúr and Karger established the existence of a sparse weighted graph G’ on the identical set of nodes with a smaller variety of edges such that with excessive chance, each reduce S’s measurement in G’ is roughly the identical as its measurement in G. This concept is illustrated beneath, the place the unique graph consists of two full graphs related by a single edge (i.e., the dumbbell graph), and the sparsified graph has fewer, however bigger weight, edges, whereas all of the reduce sizes are roughly preserved.
Illustration of the reduce preserving graph sparsification.
To algorithmically assemble such a sparser graph, Benczúr and Karger used the method of sampling edges independently, the place every edge in G is included in G’ with some chance, and its weight in G’ is scaled up by the reciprocal of the sampling chance (e.g., an fringe of authentic weight 1 in G would have a weight of 10 in G’ if it’s included with a 10% likelihood). It seems that with excessive chance, this remarkably easy (and nearly-linear time) methodology can efficiently assemble a cut-preserving graph sparsification.
The cut-preserving graph sparsification, together with a number of different artistic algorithmic concepts, yielded Karger’s breakthrough consequence. Nonetheless, Karger’s algorithm is a Monte Carlo algorithm, i.e., the output could also be incorrect with (small) chance, and there’s no recognized option to inform if the output is appropriate apart from evaluating it with an precise recognized min-cut. Since then, researchers have been on the search to resolve the open query of a nearly-linear time deterministic algorithm. Specifically, the development of the cut-preserving graph sparsification is the one element in Karger’s algorithm that’s randomized, and an obvious recipe is to discover a deterministic building (a.okay.a. derandomization) of the sparsification in nearly-linear time.
In 2015, Kawarabayashi and Thorup achieved a serious milestone with such a deterministic nearly-linear time algorithm for easy graphs, i.e., graphs which have at most one edge between each pair of nodes and all edge weights equal to 1. The important thing remark in that work is a connection between min-cut and one other necessary graph construction often known as a low-conductance reduce (defined beneath). This connection additionally turned out to be important in later efforts to derandomize Karger’s algorithm on graphs of common edge weights, which ultimately culminated in our consequence.
Alignment of min-cut and low-conductance reduce
The conductance of a reduce S is outlined because the ratio of the reduce measurement of S over the quantity of S (assuming S is the smaller quantity aspect of the reduce and is non-empty), the place the quantity of S is the sum of the diploma of the nodes in S. A reduce S of low conductance intuitively captures a bottleneck in a community, as there may be solely a small variety of edges (relative to its quantity) connecting S to the remainder of the graph. The conductance of a graph is outlined because the min conductance of any reduce within the graph, and a graph of enormous conductance (a.okay.a. an expander graph) is taken into account well-connected as there isn’t any bottleneck inside.
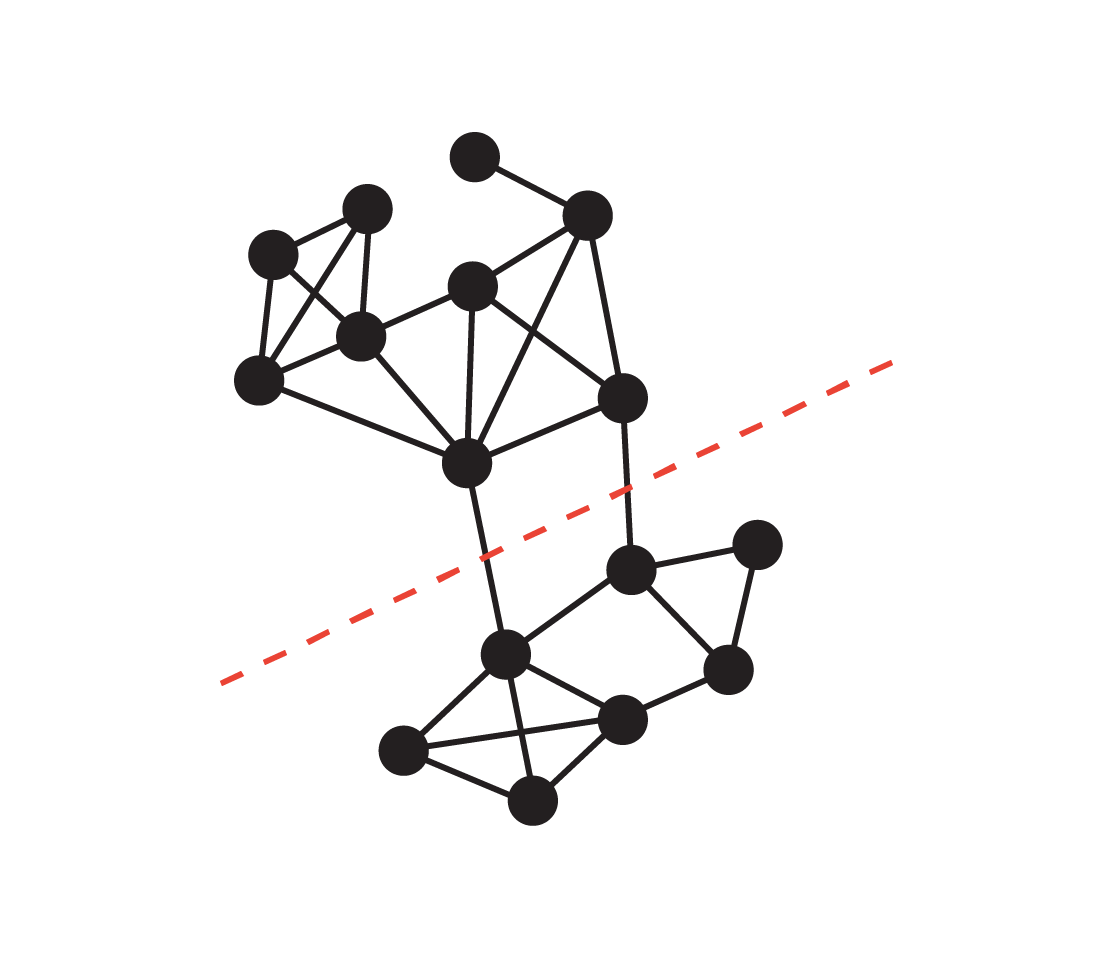
The reduce represented by the crimson dotted line has measurement 2, and the smaller aspect (the underside) has quantity 24, so its conductance is 1/12, which can be the graph’s conductance.
Kawayabarashi and Thorup made the remark that any non-trivial (i.e., either side have at the very least two nodes) min-cut should have low conductance in a easy graph the place the min node diploma is giant. Following this remark, if one can partition the graph into well-connected clusters, the partitioning have to be according to each non-trivial min-cut within the sense that every cluster should lie completely on one aspect of each such reduce. One can then contract every cluster right into a single node, and work on the smaller graph the place all non-trivial min-cuts of the unique graph are intact.
Nonetheless, for weighted graphs the identical remark not holds, and the identical partitioning used within the easy graph case will not be precisely according to non-trivial min-cuts. Nonetheless, Li 2021 noticed that such a partitioning remains to be roughly according to non-trivial min-cuts as illustrated within the determine beneath. Specifically, for a non-trivial min-cut S, there exists a reduce S’ that isn’t too completely different from S such that S’ is according to the clusters. Li additional noticed that this property of the partitioning may be exploited to effectively derandomize the development of cut-preserving graph sparsification.
A partitioning of the graph that’s roughly according to near-minimum cuts.
In our new consequence, we devise an algorithm to assemble such a partitioning tailor-made to our use case of discovering min-cut. In comparison with the extra generic off-the-shelf methodology utilized by Li within the earlier work, our tailor-made building is rather more exact, in order that the unique min-cut S and its corresponding cluster-consistent reduce S’ (within the determine above) are assured to have extra related reduce sizes. Furthermore, our algorithm is quicker than off-the-shelf strategies, which comes by bettering earlier clustering methods developed solely for easy graphs (by Henzinger, Rao and Wang in 2017) to work extra broadly on weighted graphs. The stronger precision and operating time ensures achieved by the brand new building finally result in our nearly-linear time deterministic algorithm for the min-cut drawback.
Acknowledgements
We’re grateful to our co-authors Monika Henzinger, Jason Li, and Satish Rao. We might additionally like to increase particular due to John Guilyard for creating the animation used on this submit.

