Constructing Environment friendly Neural Networks with JAX

Flax is a sophisticated neural community library constructed on prime of JAX, aimed toward giving researchers and builders a versatile, high-performance toolset for constructing complicated machine studying fashions. Flax’s seamless integration with JAX permits automated differentiation, Simply-In-Time (JIT) compilation, and assist for {hardware} accelerators, making it supreme for each experimental analysis and manufacturing.

This weblog will discover Flax’s core options, evaluate them to different frameworks, and supply a sensible instance utilizing Flax’s useful programming strategy.

Studying Goal

• Perceive Flax as a high-performance, versatile neural community library constructed on JAX appropriate for analysis and manufacturing.
• Learn the way Flax’s useful programming strategy improves the reproducibility and debugging of machine-learning fashions.
• Discover Flax’s Linen API for effectively constructing and managing complicated neural community architectures.
• Uncover the mixing of Flax with Optax for streamlined optimization and gradient processing in coaching workflows.
• Acquire insights into Flax’s parameter administration, state dealing with, and mannequin serialization for higher deployment and persistence.

This text was revealed as part of the Knowledge Science Blogathon.

What’s Flax?

Flax is a high-performance neural community library constructed on prime of JAX, designed to supply researchers and builders with the flexibleness and effectivity wanted to construct cutting-edge machine studying fashions. Flax leverages JAX’s capabilities, similar to automated differentiation and Simply-In-Time (JIT) compilation, to supply a strong framework for each analysis and manufacturing environments.

The Comparability: Flax vs. Different Frameworks

Flax distinguishes itself from different deep studying frameworks like TensorFlow, PyTorch, and Keras via its distinctive design ideas:

• Useful Programming Paradigm: Flax embraces a purely useful type, treating fashions as pure capabilities with out hidden states. This strategy enhances reproducibility and ease of debugging.
• Composability with JAX: By leveraging JAX’s transformations (jit, grad, vmap), Flax permits for seamless optimization and parallelization of mannequin computations.
• Modularity: Flax’s module system promotes the development of reusable parts, making it simpler to assemble complicated architectures from easy constructing blocks.
• Efficiency: Constructed on JAX, Flax inherits its high-performance capabilities, together with assist for {hardware} accelerators like GPUs and TPUs.

Key Options of Flax

• Linen API: Flax’s high-level API for outlining neural community layers and fashions emphasises readability and ease of use.
• Parameter Administration: Environment friendly dealing with of mannequin parameters utilizing immutable knowledge constructions, selling useful purity.
• Integration with Optax: Seamless compatibility with Optax, a gradient processing and optimization library for JAX.
• Serialization: Sturdy instruments for saving and loading mannequin parameters, facilitating mannequin persistence and deployment.
• Extensibility: Capacity to create customized modules and combine them with different JAX-based libraries.

Additionally learn: Flax

Setting Up the Atmosphere

Earlier than constructing fashions with Flax, it’s important to arrange your improvement surroundings with the mandatory libraries. We’ll set up the newest variations of JAX, JAXlib, and Flax. JAX is the spine that gives high-performance numerical computing, whereas Flax builds upon it to supply a versatile neural community framework.

# Set up the newest JAXlib model.
!pip set up --upgrade -q pip jax jaxlib
# Set up Flax at head:
!pip set up --upgrade -q git+https://github.com/google/flax.git


import jax
from typing import Any, Callable, Sequence
from jax import random, numpy as jnp
import flax
from flax import linen as nn

Clarification:

• JAX and JAXlib: JAX is a library for high-performance numerical computing and automated differentiation, whereas JAXlib gives the low-level implementations required by JAX.
• Flax: A neural community library constructed on prime of JAX, providing a versatile and environment friendly API for constructing fashions.
• Flax’s Linen API: Imported as nn, Linen is Flax’s high-level API for outlining neural community layers and fashions.

Flax Fundamentals: Linear Regression Instance

Linear regression is a foundational machine studying method used to mannequin the connection between a dependent variable and a number of unbiased variables. In Flax, we will implement linear regression utilizing a single dense (totally related) layer.

Mannequin Instantiation

First, let’s instantiate a dense layer with Flax’s Linen API.

# We create one dense layer occasion (taking 'options' parameter as enter)
mannequin = nn.Dense(options=5)

Clarification:

• nn.Dense: Represents a dense (totally related) neural community layer with a specified variety of output options. Right here, we’re making a dense layer with 5 output options.

Parameter Initialization

In Flax, mannequin parameters usually are not saved inside the mannequin itself. As a substitute, you should initialize them utilizing a random key and dummy enter knowledge. This course of leverages Flax’s lazy initialization, the place parameter shapes are inferred based mostly on the enter knowledge.

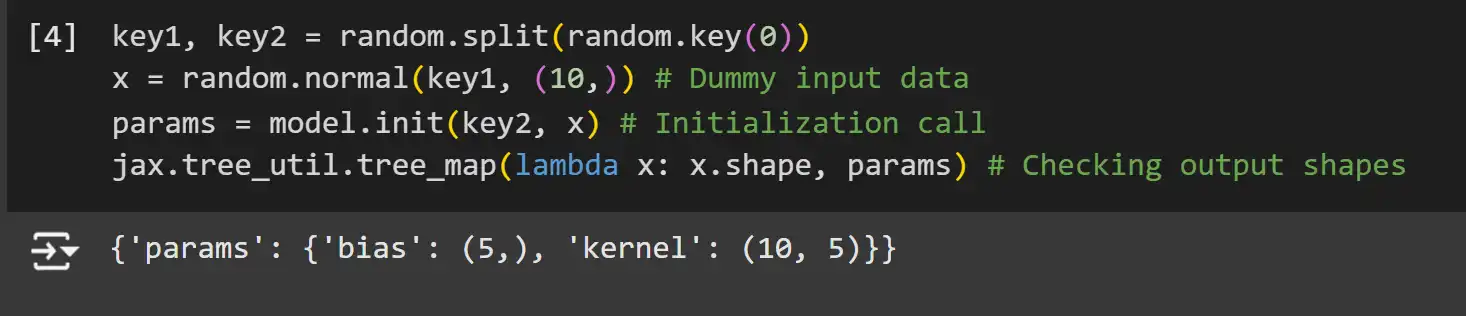
key1, key2 = random.break up(random.key(0))
x = random.regular(key1, (10,)) # Dummy enter knowledge
params = mannequin.init(key2, x) # Initialization name
jax.tree_util.tree_map(lambda x: x.form, params) # Checking output shapes

Clarification:

• Random Key Splitting: JAX makes use of pure capabilities and handles randomness by way of express PRNG keys. We break up the preliminary key into two for unbiased random quantity technology.
• Dummy Enter Knowledge: A dummy enter x with form (10,) is used to set off form inference throughout parameter initialization.
• mannequin.init: Initializes the mannequin’s parameters based mostly on the enter knowledge form and the random key.
• tree_map: Applies a perform to every leaf within the parameter tree to examine shapes.

Be aware: JAX and Flax, like NumPy, are row-based programs, that means that vectors are represented as row vectors and never column vectors. This may be seen within the form of the kernel right here.

Ahead Go

After initializing the parameters, you may carry out a ahead go to compute the mannequin’s output for a given enter.

mannequin.apply(params, x)

Clarification:

• mannequin.apply: Executes the mannequin’s ahead go utilizing the offered parameters and enter knowledge.

Gradient Descent Coaching

With the mannequin initialized, we will carry out gradient descent to coach our linear regression mannequin. We’ll generate artificial knowledge and outline a imply squared error (MSE) loss perform.

# Set drawback dimensions.
n_samples = 20
x_dim = 10
y_dim = 5

# Generate random floor fact W and b.
key = random.key(0)
k1, k2 = random.break up(key)
W = random.regular(k1, (x_dim, y_dim))
b = random.regular(k2, (y_dim,))
# Retailer the parameters in a FrozenDict pytree.
true_params = flax.core.freeze({'params': {'bias': b, 'kernel': W}})

# Generate samples with further noise.
key_sample, key_noise = random.break up(k1)
x_samples = random.regular(key_sample, (n_samples, x_dim))
y_samples = jnp.dot(x_samples, W) + b + 0.1 * random.regular(key_noise, (n_samples, y_dim))
print('x form:', x_samples.form, '; y form:', y_samples.form)

Clarification:

• Downside Dimensions: Defines the variety of samples (n_samples), enter dimension (x_dim), and output dimension (y_dim).
• Floor Reality Parameters: Randomly initializes the true weights W and biases b used to generate artificial goal knowledge.
• FrozenDict: Flax makes use of FrozenDict to make sure immutability of parameters.
• Knowledge Technology: Creates artificial enter knowledge x_samples and goal knowledge y_samples with added noise to simulate real-world situations.

Defining the MSE Loss Perform

Subsequent, we’ll outline the imply squared error (MSE) loss perform and carry out gradient descent utilizing JAX’s JIT compilation for effectivity.

# Outline the MSE loss perform.
@jax.jit
def mse(params, x_batched, y_batched):
    # Outline the squared loss for a single pair (x, y)
    def squared_error(x, y):
        pred = mannequin.apply(params, x)
        return jnp.interior(y - pred, y - pred) / 2.0
    # Vectorize the earlier to compute the common of the loss on all samples.
    return jnp.imply(jax.vmap(squared_error)(x_batched, y_batched), axis=0)

Clarification:

• @jax.jit: JIT-compiles the mse perform for optimized efficiency.
• squared_error: Computes the squared error between predictions and true values.
• jax.vmap: Vectorizes the squared_error perform to use it throughout all samples effectively.
• Imply Squared Error: Calculates the common loss over all samples.

Gradient Descent Parameters and Replace Perform

We’ll set the training price and outline capabilities to compute gradients and replace mannequin parameters.

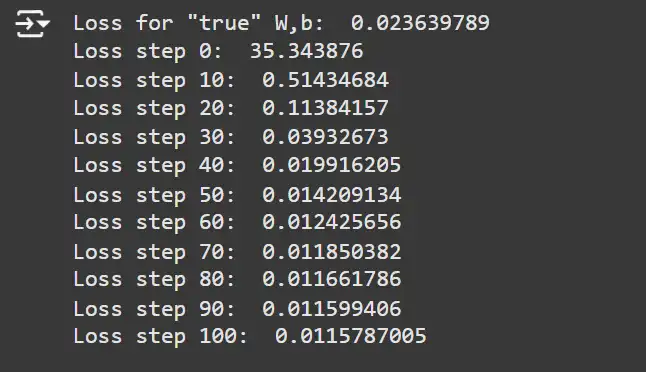
learning_rate = 0.3  # Gradient step dimension.
print('Loss for "true" W,b: ', mse(true_params, x_samples, y_samples))
loss_grad_fn = jax.value_and_grad(mse)

@jax.jit
def update_params(params, learning_rate, grads):
  params = jax.tree_util.tree_map(
      lambda p, g: p - learning_rate * g, params, grads)
  return params

for i in vary(101):
  # Carry out one gradient replace.
  loss_val, grads = loss_grad_fn(params, x_samples, y_samples)
  params = update_params(params, learning_rate, grads)
  if i % 10 == 0:
    print(f'Loss step {i}: ', loss_val)

Clarification:

• Studying Fee: Determines the step dimension throughout parameter updates.
• loss_grad_fn: Makes use of jax.value_and_grad to compute each the loss worth and its gradients with respect to the parameters.
• update_params: Updates the mannequin parameters by subtracting the product of the training price and gradients.

Coaching Loop

Lastly, we’ll execute the coaching loop, performing parameter updates and monitoring the loss.

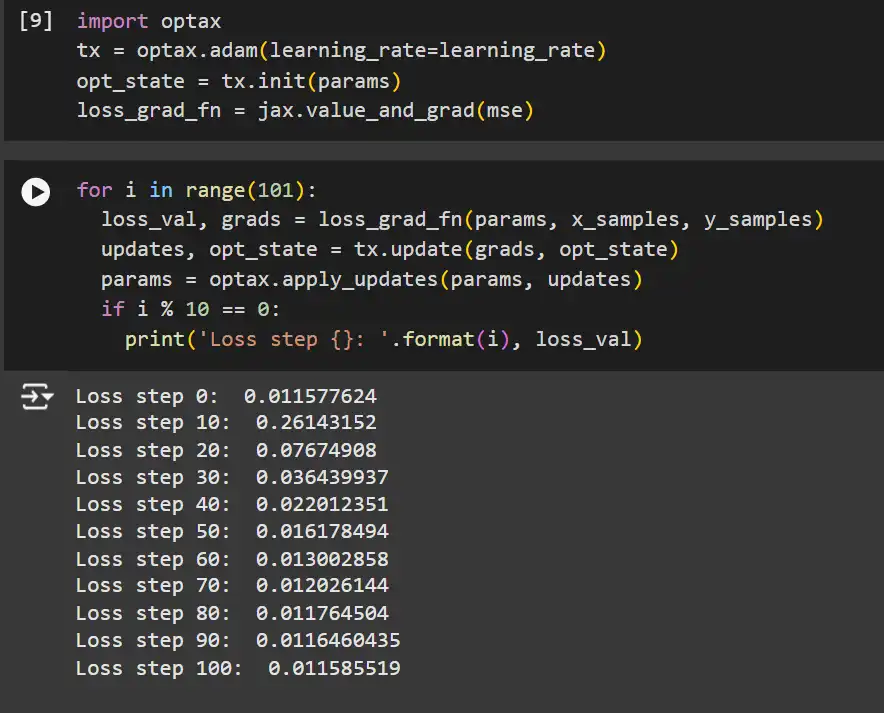
import optax
tx = optax.adam(learning_rate=learning_rate)
opt_state = tx.init(params)
loss_grad_fn = jax.value_and_grad(mse)

for i in vary(101):
  loss_val, grads = loss_grad_fn(params, x_samples, y_samples)
  updates, opt_state = tx.replace(grads, opt_state)
  params = optax.apply_updates(params, updates)
  if i % 10 == 0:
    print('Loss step {}: '.format(i), loss_val)

Clarification:

• Optax Optimizer: Initializes the Adam optimizer with the desired studying price.
• Optimizer State: Maintains the state required by the optimizer (e.g., momentum phrases for Adam).
• tx.replace: Computes parameter updates based mostly on gradients and the optimizer state.
• optax.apply_updates: Applies the computed updates to the mannequin parameters.
• Coaching Loop: Iterates via coaching steps, updating parameters and monitoring loss.

Advantages of Utilizing Optax:

• Simplicity: Abstracts away handbook gradient updates, decreasing boilerplate code.
• Flexibility: Helps a variety of optimization algorithms and gradient transformations.
• Composability: Permits composing easy gradient transformations into extra complicated optimizers.

Serialization: Saving and Loading Fashions

After coaching, you might wish to save your mannequin’s parameters for later use or deployment. Flax gives sturdy serialization utilities to facilitate this course of.

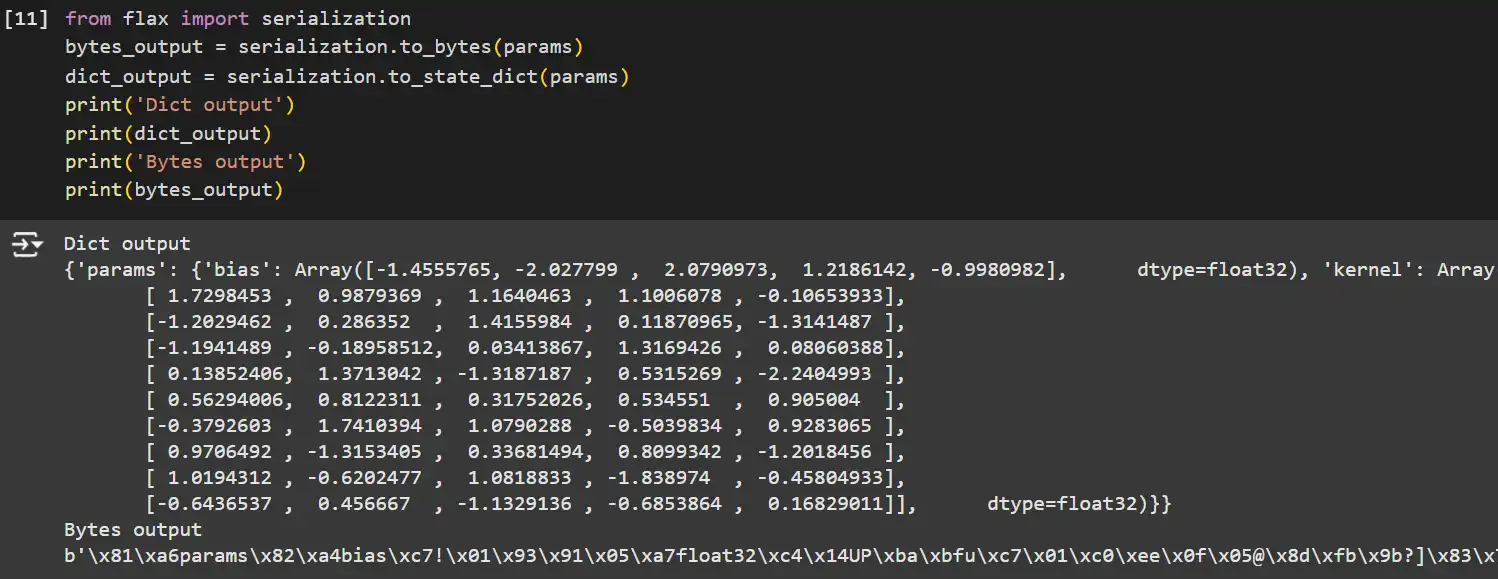
from flax import serialization

# Serialize parameters to bytes.
bytes_output = serialization.to_bytes(params)
# Serialize parameters to a dictionary.
dict_output = serialization.to_state_dict(params)

print('Dict output')
print(dict_output)
print('Bytes output')
print(bytes_output)

Clarification:

• serialization.to_bytes: Converts the parameter tree to a byte string, appropriate for storage or transmission.
• serialization.to_state_dict: Converts the parameter tree to a dictionary, making it simple to save lots of as JSON or different human-readable codecs.

Deserializing the Mannequin

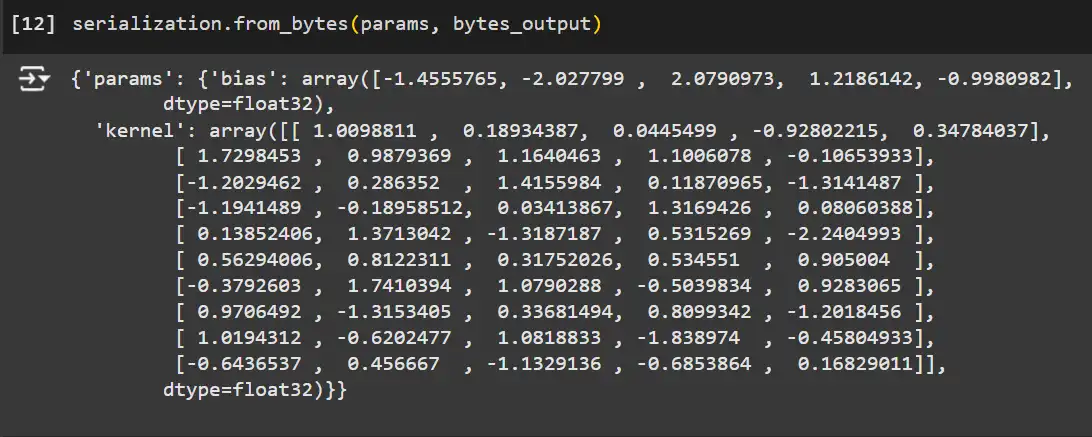
Utilizing the from_bytes technique with a parameter template to load the mannequin parameters again.

# Load the mannequin again utilizing the serialized bytes.
loaded_params = serialization.from_bytes(params, bytes_output)

Defining Customized Fashions

Flax’s flexibility shines when defining customized fashions past easy linear regressions. This part’ll discover methods to create customized multi-layer perceptrons (MLPs) and handle state inside your fashions.

Module Fundamentals

Modules in Flax are subclasses of nn.Module and characterize layers or total fashions. Right here’s methods to outline a customized MLP with a sequence of dense layers and activation capabilities.

class ExplicitMLP(nn.Module):
  options: Sequence[int]

  def setup(self):
    # we robotically know what to do with lists, dicts of submodules
    self.layers = [nn.Dense(feat) for feat in self.features]
    # for single submodules, we might simply write:
    # self.layer1 = nn.Dense(feat1)

  def __call__(self, inputs):
    x = inputs
    for i, lyr in enumerate(self.layers):
      x = lyr(x)
      if i != len(self.layers) - 1:
        x = nn.relu(x)
    return x

key1, key2 = random.break up(random.key(0), 2)
x = random.uniform(key1, (4,4))

mannequin = ExplicitMLP(options=[3,4,5])
params = mannequin.init(key2, x)
y = mannequin.apply(params, x)

print('initialized parameter shapes:n', jax.tree_util.tree_map(jnp.form, flax.core.unfreeze(params)))
print('output:n', y)

Clarification:

• ExplicitMLP: A easy multi-layer perceptron with specified options for every layer.
• setup(): Register’s submodules (dense layers) that Flax tracks for parameter initialization and serialization.
• __call__(): Defines the ahead go, making use of every layer and a ReLU activation apart from the final layer.

Trying to name the mannequin immediately with out utilizing apply will end in an error:

strive:
    y = mannequin(x)  # Returns an error
besides AttributeError as e:
    print(e)

Clarification:

• mannequin.apply: Flax’s useful API requires making use of to execute the mannequin’s ahead go with given parameters.

Utilizing the @nn.compact Decorator

Another and extra concise option to outline submodules is by utilizing the @nn.compact decorator inside the __call__ technique.

class SimpleMLP(nn.Module):
  options: Sequence[int]

  @nn.compact
  def __call__(self, inputs):
    x = inputs
    for i, feat in enumerate(self.options):
      x = nn.Dense(feat, title=f'layers_{i}')(x)
      if i != len(self.options) - 1:
        x = nn.relu(x)
      # offering a reputation is elective although!
      # the default autonames could be "Dense_0", "Dense_1", ...
    return x

key1, key2 = random.break up(random.key(0), 2)
x = random.uniform(key1, (4,4))

mannequin = SimpleMLP(options=[3,4,5])
params = mannequin.init(key2, x)
y = mannequin.apply(params, x)

print('initialized parameter shapes:n', jax.tree_util.tree_map(jnp.form, flax.core.unfreeze(params)))
print('output:n', y)

Clarification:

• @nn.compact: A decorator that permits defining submodules and parameters inside the __call__ technique, enabling a extra concise and readable mannequin definition.
• Naming Submodules: Optionally gives names to submodules for readability; in any other case, Flax auto-generates names like “Dense_0”, “Dense_1”, and many others.

Variations Between setup and @nn.compact:

• setup Methodology:
  • Permits defining submodules exterior the __call__ technique.
  • Helpful for modules with a number of strategies or dynamic constructions.
• @nn.compact Decorator:
  • Allows defining submodules inside the __call__ technique.
  • Extra concise for easy and glued architectures.

Module Parameters

Generally, you would possibly must outline customized layers not offered by Flax. Right here’s methods to create a easy dense layer from scratch utilizing the @nn.compact strategy.

class SimpleDense(nn.Module):
    options: int
    kernel_init: Callable = nn.initializers.lecun_normal()
    bias_init: Callable = nn.initializers.zeros_init()

    @nn.compact
    def __call__(self, inputs):
        kernel = self.param('kernel',
                            self.kernel_init,  # Initialization perform
                            (inputs.form[-1], self.options))  # Form information.
        y = jnp.dot(inputs, kernel)
        bias = self.param('bias', self.bias_init, (self.options,))
        y = y + bias
        return y

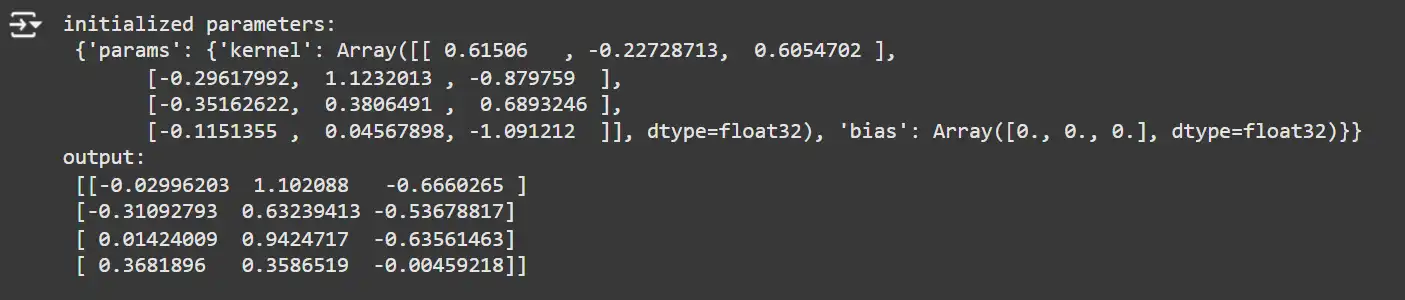
key1, key2 = random.break up(random.key(0), 2)
x = random.uniform(key1, (4, 4))

mannequin = SimpleDense(options=3)
params = mannequin.init(key2, x)
y = mannequin.apply(params, x)

print('initialized parameters:n', params)
print('output:n', y)

Clarification:

• Customized Parameters: Makes use of self.param to register customized parameters (kernel and bias).
• Initialization Features: Specifies how every parameter is initialized.
• Guide Computation: Performs the dense computation manually utilizing jnp.dot.

Key Factors:

• self.param: Registers a parameter with a reputation, initialization perform, and form.
• Guide Parameter Administration: Supplies granular management over parameter definitions and initializations.

Variables and Collections of Variables

Along with parameters, neural networks typically keep state variables, similar to working statistics in batch normalization. Flax lets you handle these variables utilizing the variable technique.

Instance: Bias Adder with Working Imply

class BiasAdderWithRunningMean(nn.Module):
    decay: float = 0.99

    @nn.compact
    def __call__(self, x):
        # Examine if 'imply' variable is initialized.
        is_initialized = self.has_variable('batch_stats', 'imply')
        # Initialize working common of the imply.
        ra_mean = self.variable('batch_stats', 'imply',
                                lambda s: jnp.zeros(s),
                                x.form[1:])
        # Initialize bias parameter.
        bias = self.param('bias', lambda rng, form: jnp.zeros(form), x.form[1:])
        if is_initialized:
            ra_mean.worth = self.decay * ra_mean.worth + (1.0 - self.decay) * jnp.imply(x, axis=0, keepdims=True)

        return x - ra_mean.worth + bias

# Initialize and apply the mannequin.
key1, key2 = random.break up(random.key(0), 2)
x = jnp.ones((10, 5))
mannequin = BiasAdderWithRunningMean()
variables = mannequin.init(key1, x)
print('initialized variables:n', variables)
y, updated_state = mannequin.apply(variables, x, mutable=['batch_stats'])
print('up to date state:n', updated_state)

Clarification:

• self.variable: Registers a mutable variable (imply) beneath the ‘batch_stats’ assortment.
• State Initialization: Initializes working imply with zeros.
• State Replace: Updates the working imply throughout the ahead go if already initialized.
• Mutable State: Specifies which collections are mutable throughout the ahead go utilizing the mutable argument in apply.

Managing Optimizer and Mannequin State

Dealing with each parameters and state variables (like working means) could be complicated. Right here’s an instance of integrating parameter updates with state variable updates utilizing Optax.

for val in [1.0, 2.0, 3.0]:
  x = val * jnp.ones((10,5))
  y, updated_state = mannequin.apply(variables, x, mutable=['batch_stats'])
  old_state, params = flax.core.pop(variables, 'params')
  variables = flax.core.freeze({'params': params, **updated_state})
  print('up to date state:n', updated_state) # Reveals solely the mutable half

from functools import partial

@partial(jax.jit, static_argnums=(0, 1))
def update_step(tx, apply_fn, x, opt_state, params, state):

  def loss(params):
    y, updated_state = apply_fn({'params': params, **state},
                                x, mutable=checklist(state.keys()))
    l = ((x - y) ** 2).sum()
    return l, updated_state

  (l, state), grads = jax.value_and_grad(loss, has_aux=True)(params)
  updates, opt_state = tx.replace(grads, opt_state)
  params = optax.apply_updates(params, updates)
  return opt_state, params, state

x = jnp.ones((10,5))
variables = mannequin.init(random.key(0), x)
state, params = flax.core.pop(variables, 'params')
del variables
tx = optax.sgd(learning_rate=0.02)
opt_state = tx.init(params)

for _ in vary(3):
  opt_state, params, state = update_step(tx, mannequin.apply, x, opt_state, params, state)
  print('Up to date state: ', state)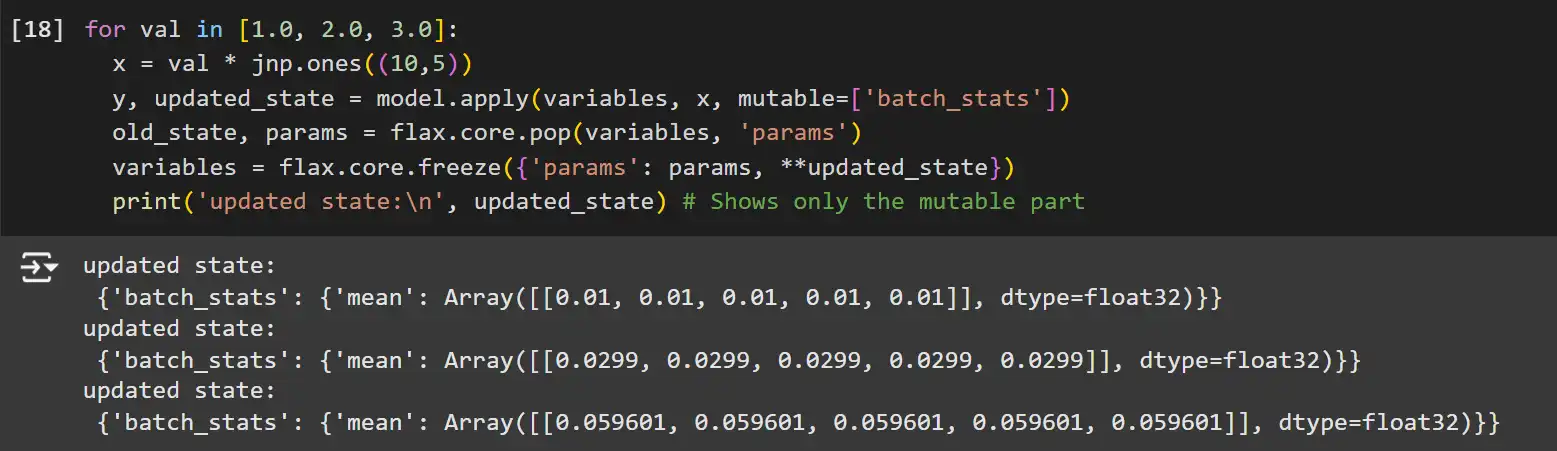

Clarification:

• update_step Perform: A JIT-compiled perform that updates each parameters and state variables.
• Loss Perform: Computes the loss and updates state variables concurrently.
• Gradient Computation: Makes use of jax.value_and_grad to compute gradients with respect to parameters.
• Optax Updates: Applies optimizer updates to the parameters.
• Coaching Loop: Iterates via coaching steps, updating parameters and state variables.

Be aware: The perform signature could be verbose and will not work with jax.jit() immediately as a result of some perform arguments usually are not “legitimate JAX varieties.” Flax gives a handy wrapper known as TrainState to simplify this course of. Consult with flax.coaching.train_state.TrainState for extra info.

Exporting to TensorFlow’s SavedModel with jax2tf

JAX launched an experimental converter known as jax2tf, which permits changing skilled Flax fashions into TensorFlow SavedModel format (so it may be used for TF Hub, TF.lite, TF.js, or different downstream functions). The repository accommodates extra documentation and has varied examples for Flax.

Conclusion

Flax is a flexible and highly effective neural community library that leverages JAX’s high-performance capabilities. From organising easy linear regression fashions to defining complicated customized architectures and managing state, Flax gives a versatile framework for analysis and manufacturing environments.

On this information, we lined:

• Atmosphere Setup: Putting in JAX, JAXlib, and Flax.
• Linear Regression: Implementing and coaching a easy linear mannequin.
• Optimization with Optax: Streamlining the coaching course of utilizing superior optimizers.
• Serialization: Saving and loading mannequin parameters effectively.
• Customized Fashions: Constructing customized neural community architectures with state administration.

By mastering these fundamentals, you’re well-equipped to harness Flax’s full potential in your machine-learning tasks. Whether or not you’re conducting tutorial analysis, growing production-ready fashions, or exploring revolutionary architectures, Flax affords the instruments and suppleness to assist your endeavours.

Additionally, if you’re in search of an AI/ML course on-line, then discover: Licensed AI & ML BlackBelt PlusProgram

Key Takeaways

1. Flax is a versatile, high-performance neural community library constructed on JAX, providing modularity and composability for deep studying fashions.
2. It follows a useful programming paradigm, enhancing fashions’ reproducibility, debugging, and maintainability.
3. Flax integrates seamlessly with JAX, using its optimization and parallelization capabilities for high-speed computation.
4. The Linen API and `@nn.compact` decorator simplify defining and managing neural community layers and parameters.
5. Flax gives utilities for state administration, mannequin serialization, and environment friendly coaching utilizing composable optimizers like Optax.

The media proven on this article shouldn’t be owned by Analytics Vidhya and is used on the Creator’s discretion.

Incessantly Requested Questions

My title is Nilesh Dwivedi, and I am excited to affix this vibrant neighborhood of bloggers and readers. I am at the moment in my first yr of BTech, specializing in Knowledge Science and Synthetic Intelligence at IIIT Dharwad. I am captivated with expertise and knowledge science and looking out ahead to put in writing extra blogs.